Ha a cím alapján arra gondolnánk, hogy előkerült Erich Kästner egyik elveszettnek hitt regénye, tévednénk. Hujter Bálint, Lenger Dániel és Szűcs Gábor közelmúltban megjelent könyve, a Hajók, festmények, nagymamák ugyanis matematikai kalandozásra invitálja az olvasót.

A három szerzőt sok éve jól ismerem, és az általuk képviselt matematikatanítási felfogás is nagyon közel áll hozzám. Ezért elképzelhető, hogy elfogult vagyok velük szemben, amit érdemes idejében leszögezni.

A mű 13+1 fejezetből áll, minden fejezet 6 feladatot tartalmaz, vagyis 84 kellemes, szórakoztató, olykor hosszú és komoly fejtörést igénylő matematikai probléma elé állítja az olvasót. A feladatok jelentős részéhez bőven elegendő az általános iskolában tanult matematika, de sok esetben kitartó gondolkodásra van szükség. Olykor nem árt, ha rendelkezésre áll komoly kreativitás, ötletesség, olykor pedig a feladat teremtette helyzet precíz elemzése, és az abban való eligazodás segít. Az utolsó néhány feladat már kifejezetten nehéz, szinte mindenkit komoly gondolkodásra késztet.

A könyv feladatainak jelentős részét a szerzők, illetve a Dürer Verseny szervezői találták ki, vagyis ez alapvetően nem egy válogatás mások feladataiból. Ez persze nem jelenti azt, hogy nincs benne olyan feladat, amit ne ismerhetne máshonnan is az olvasó.

A Dürer Verseny Szűcs Gábor és Farkas Ádám ötlete nyomán indult el, és mára a diákok egyik kedvenc csapatversenye az országban. Ötödiktől nyolcadik osztályig Borsod-Abaúj-Zemplén, Szabolcs-Szatmár-Bereg és Heves megye iskoláinak tanulói vehetnek részt a versenyben, a kilencedik-tizenkettedik osztályok számára szervezett versenyen viszont már nincs ilyen korlátozás, bárki elindulhat. A szabályok megkövetelik, hogy lányok is legyenek a csapatokban, illetve a kategóriák meghatározásánál a korábbi évek versenyeredményeit is figyelembe veszik, ezzel évről évre megteremtik a lehetőséget, hogy újabb és újabb diákoknak legyen komoly esélye a jó eredmény elérésére. Akit ennél részletesebben érdekel a verseny, annak ajánlott felkeresni a honlapjukat.

A matematikai feladatgyűjtemények szerzőinek többsége vélhetően azt a célt tartja szeme előtt, hogy az olvasó gondolkozzon a feladatokon, és ne lapozzon azonnal a Megoldások részhez, de ez a szerzőhármas különösen nagy gondot fordít erre a szemléletre. A könyvben persze nem tudják megakadályozni az olvasót, hogy hátralapozzon, de amikor tanítanak, akkor komoly erőfeszítést tesznek azért, hogy minél többen, minél több megoldást, saját maguk találjanak ki. Ez a szemlélet a könyvükön is tükröződik, és nagyon bízom benne, hogy az olvasók megfogadják a szerzők tanácsát, és kitartóan gondolkoznak a feladatokon, mielőtt az ötletekhez, majd a megoldásokhoz lapoznának.

Egy-egy fejezet akár egy-egy szakkör anyaga is lehet, de a normál iskolai oktatásban is fel lehet használni a problémákat. Több esetben is visszatér egy feladat nehezebb formában, vagy egy korábban hasznosnak bizonyult gondolat, megközelítés egy későbbi feladatnál is segít a megoldásban.

A Megoldások fejezet lényegesen több a megoldások puszta közlésénél. Rendszeresen előfordul, hogy egy feladat kapcsán több megoldást is olvashatunk, és arra is találunk példát, hogy hibás gondolatmenetet közölnek a szerzők. Egy hibás gondolatmenetből is nagyon sokat tanulhatunk, nem egy esetben egy rossz megoldás, és a benne lévő hiba megértése lényegesen hozzájárul ahhoz, hogy a jó megoldást még jobban megértsük. Olykor általánosítás, illetve csatlakozó kérdés felvetése is megjelenik a feladat megoldása után.

Minden fejezet utolsó feladata egy kétszemélyes, stratégiás játék. Feltételezhető, hogy a szerzők is fontos eszköznek tartják az ilyen típusú problémákat a matematikaoktatásban, hiszen 14 különböző játék szerepel a könyvben. Az ilyen játékok nagy motivációt jelentenek a diákoknak, nagyon szívesen gondolkoznak rajtuk. Ketten érdemes megfejteni a stratégiát, hiszen ketten könnyű játszani a játékokat. Ebből kifolyólag a hatékony közös munka fejlesztésére is kiválóan alkalmasak. Az is indokolja, hogy minden fejezetben szerepel egy ilyen játék, mert a Dürer Verseny döntőjében is hagyományosan minden évben az egyik feladat egy stratégiás játék elemzése, ahol a jó megoldást úgy kell bizonyítani, hogy le kell győzni a játékban a verseny szervezőit.

Számomra a feladatok azért is voltak nagyon szórakoztatóak, mert rendszeresen valamilyen kedves történetbe vannak ágyazva, sokszor ötletes elnevezések jelennek meg bennük (személyes kedvencem a babonapehely), és nem egyszer irodalmi, képzőművészeti utalásokkal is találkozhatunk.

Ízelítőül és kedvcsinálás gyanánt álljon itt két feladat a könyvből, közülük az egyik egy stratégiás játék, hiszen azoknak kiemelt szerep jut a könyvben is.

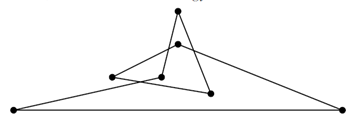
• Egy hurkolt sokszöget egyszeresen önmetszőnek nevezünk, ha mindegyik oldala pontosan egy másik oldalát metszi, és egyetlen oldala sem megy át a végeitől különböző csúcson.
  • a) Rajzolj egy egyszeresen önmetsző hurkolt sokszöget.
  • b) Legkevesebb hány oldala lehet egy ilyen sokszögnek?

Az alábbi ábra egy olyan hurkolt hétszöget mutat be, amely sajnos nem egyszeresen önmetsző, mivel az alsó oldala egyetlen másik oldalt sem metsz.

• Két kupac korong van az asztalon. Két játékos felváltva lép a következő módon:

a soron lévő előbb az egyik kupacot teljes egészében kiveszi a játékból, majd a másik kupacot szétosztja két kisebb kupacra. Szétosztani csak olyan kupacot lehet, amelyben legalább két korong van. Egy lépést követően tehát újra két kupac marad, mindegyikben legalább egy korong. Az a játékos veszít, aki nem tud szabályosan lépni.

Hogyan érdemes játszani ezt a játékot, ha a kezdőhelyzet ismeretében eldöntheted, hogy kezdeni szeretnél, vagy átadod a kezdés jogát?

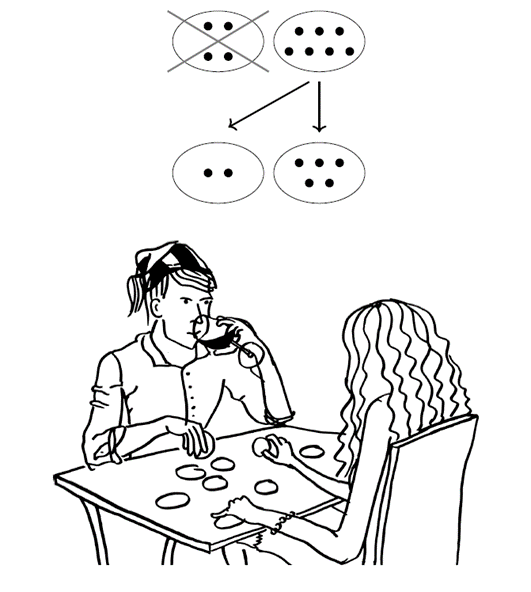
Ahogy a két példából is látszik, a feladatokhoz remek illusztrációk is tartoznak, amik Szűcs Júlia munkáját dicsérik.

Számomra a könnyebb használatot segítette volna, ha a feladatok szövege, akár kisebb betűmérettel, de újra megjelenik a megoldások előtt is.

A könyv nagyszerű forrás matematikaszakkörök anyagához, de az iskolai tananyagba is jól beépíthető feladatokat tartalmaz. Ajánlom mindenkinek, aki örömmel töri a fejét szellemes, de nem feltétlenül könnyű problémákon. Garantáltan jól fog szórakozni.

Juhász Péter
Rényi Alfréd Matematikai Kutatóintézet