
Borítótervező:
Megjelenés: 2022. 01. 13.
Oldalszám: 216 oldal
Formátum: A/5
ISBN: 978-963-4931-65-2
Témakör: Matematikatörténet, -filozófia, népszerűsítés, Tudománytörténet, Matematika, Történelem
Eredeti ár: 3900 Ft
Webshop ár: 2925 Ft
KOSÁRBA
Gondolatok Mark Kac önéletrajzáról
Nemrég kaptam kölcsön Tóth Bálint barátomtól egy nagyszerű könyvet, Mark Kac: Enigmas of Chance, Harper and Row, New York, 1985 (160 oldal, unalmas előszavakkal). A nagy matematikus saját életén végigfutva, a véletlen rejtélyeivel ismerteti meg az olvasót. Ellentétben számos excentrikus matematikus önéletrajzával, Kacé biztos ízléssel és finom humorral ötvözi a különböző összetevőket: matematikát (beleértve a matematikai fizikát), történelmet, családot és a kollégákat. Pár nap alatt végigolvastam a könyvet. Minden matematikai érdeklődésű egyénnek ajánlom, de ezt egy rövid ismertetővel szeretném alátámasztani. Érdemes az olvasás előtt a Wikipédián tájékozódni M. Kacról, mert bizonyos dolgokat itt nem ismétlek el.
Kac 1914-ben született egy nyugat-ukrajnai zsidó kisvárosban, Krzemieniecben (pár évvel később Isaac Stern is itt született). A városka Lengyelország egyik felosztása után, még a 18. században Oroszországhoz került. 1918-tól újra Lengyelország, 1939/45-től 1991-ig a Szovjetunió (közben német megszállás), azóta Ukrajna része volt/lett. Kac apja Lipcsében és Moszkvában doktorált filozófiából, de tanítóként, majd kereskedőként tengette életét. Gyerekkorában Mark a jiddis mellett oroszul beszélt, majd a középiskolában megtanult lengyelül és franciául is. 16 éves korában saját bizonyítást adott a Cardano-képletre, amely megjelent a Középiskolai Matematikai Lapok ottani megfelelőjében. Ennek nyomán egy szakfelügyelő rábeszélte, hogy ne mérnök, hanem matematikus legyen.
Matematikusként a szülővárosától 150 km-re nyugatra fekvő Lemberg egyetemén tanult (Lvov, Lwów, Lviv). A város a hosszú 19. században Ausztria, utána Lengyelország stb. része volt. Magyarországhoz hasonlóan, a két világháború között a frissen függetlenné vált Lengyelországban is dúlt az antiszemitizmus: zsidópadok voltak a zsidó egyetemistáknak, s a zöldszalagosok rendszeresen megverték a zsidó diákokat. Míg a Budapesti Tudományegyetemen (akkor Pázmány Péterről volt elnevezve) csak egy nemzetközi hírű matematikus tanított (Fejér Lipót), addig a Lembergi Egyetemen több világklasszis matematikus oktatott: Banach, Steinhaus, Ulam – hogy csak a leghíresebbeket említsem.
Stefan Banach (a funkcionálanalízis egyik atyja, a Banach-terek névadója) igazi bohém volt. Az általa gyakran látogatott, ún. Skót kávéházban egy később nevezetessé vált füzetbe írták bele születő matematikai gondolataikat Banach és társai. (A német megszállás idején az egykori szupersztár egy német biológiai laboratóriumban „tetűetetőként” tengette életét, de még megélte a németek kiűzését.)
Hősünk igazi támogatója, Hugo Steinhaus is világhírű volt, Banachhal együtt ő teremtette meg a lwówi matematikai iskolát. Lebesgue mértékelméletére alapozva létrehozták a funkcionálanalízist, de ortogonális sorokra és valószínűségszámításra is alkalmazták az elvont elméletet. Szűken vett tudományos munkájával szinte egyenrangú volt nevelői munkássága. Egyaránt támogatta az élvonalbeli matematika művelését és a matematika népszerűsítését (Matematikai kaleidoszkóp c. munkája – lengyel első kiadás: 1939 – magyarul is több kiadásban megjelent: pl. 1951, 1984), de II. világháború végén a lengyeltelenített Lvov helyett a lengyelesített Wroclawban szervezte újjá az ottani egyetemet.
Kaccal nagyjából egy időben tevékenykedett Lembergben Stanislaw Ulam, aki matematikusként is kiemelkedő volt: halmaz- és mértékelméleti, valamint topológiai cikkekkel kezdte pályafutását. Jó érzékkel elfogadta Neumann életmentő amerikai meghívását: később Teller Edével együtt a hidrogénbomba feltalálásában játszott vezető szerepet. (Mellesleg Ulam is írt egy lenyűgöző – és Kaccéval párhuzamos – önéletrajzot: Adventures of a Mathematician, 1983, amelyet Kac a Bevezetésben oldalakon át méltányol.)
Kac Steinhaustól tanulta az éppen akkor kibontakozó valószínűségszámítást. Első cikkeit vele írta, és az analízisben alkalmazták az addig empirikusnak tartott Gauss-féle hibatörvényt. Mivel Kac tudományos pályáját végig kísérte a valószínűségszámítás (az önéletrajz címében is szerepel az esély szó), egy egész fejezetet szentel a témának. Az utóbbi évtizedek matematikushallgatói (beleértve a recenzenst) már a Kolmogorov-féle axiomatikus megalapozással kezdik, de 1933 előtt volt valami szakadék a valószínűségszámítás és a matematika többi területe között. Bár olyan nevek jelezték a korai valószínűségszámítást, mint Pascal, Fermat, Jakob Bernoulli, de Moivre, Gauss, Laplace, Csebisev, még Hilbert 1900-as programja is megoldandó feladatnak tűzte ki az axiomatikus megalapozást. Ma már tudjuk, hogy ehhez meg kellett születnie a mértékelméletnek (Lebesgue, 1902). Nem véletlen, hogy a nagy számok erős törvényének első változata a mértékelmélet egyik atyjától, Boreltől származik (1909), de a teljes matematikai szabatosságra még várni kellett.
Kac részletesen elmagyarázza Borel gondolatának egyik legfontosabb részletét. Dobjunk föl egymástól függetlenül egy „igazi” (nem hamis) pénzérmét elég sokszor. A törvény azt állítja, hogy mind az Fejek, mind az Írások relatív gyakorisága majdnem biztosan 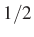 -hez tart. (Nyilvánvaló, hogy biztosat nem állíthatunk, hiszen egymás után végtelen sokszor is lehet akár csupa Fej, vagy csupa Írás sorozat – de ennek valószínűsége elhanyagolható.) Ha Fej, akkor 1-et írunk, ha Írás, akkor 0-t. Ezzel egy technikailag bonyolult valószínűségszámítási tételt egy viszonylag egyszerű mértékelméleti feladatra fordítottunk le: tekintsük a
-hez tart. (Nyilvánvaló, hogy biztosat nem állíthatunk, hiszen egymás után végtelen sokszor is lehet akár csupa Fej, vagy csupa Írás sorozat – de ennek valószínűsége elhanyagolható.) Ha Fej, akkor 1-et írunk, ha Írás, akkor 0-t. Ezzel egy technikailag bonyolult valószínűségszámítási tételt egy viszonylag egyszerű mértékelméleti feladatra fordítottunk le: tekintsük a ![$ [0,1]$](https://ematlap.hu/images/stories/latex/simonovitskac/img2.png) szakasz valós számait kettes számrendszerben; ekkor a 0 és 1-es számok relatív gyakorisága aszimptotikusan
szakasz valós számait kettes számrendszerben; ekkor a 0 és 1-es számok relatív gyakorisága aszimptotikusan 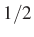 –
–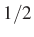 majdnem minden számra.
majdnem minden számra.
De Moivre már 1718 körül belátta, hogy 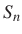 -nel jelölve az 1-esek összegét az első
-nel jelölve az 1-esek összegét az első 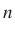 dobásban, az
dobásban, az véletlen változó eloszlása tart a Gauss-féle haranggörbéhez. Ezen az úton haladt 1923-tól Steinhaus, és ezen az úton indította el Kacot 1935 körül. Egyik közös tételüket Kac szintén részletesen bemutatja az olvasóknak. Legyenek
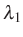 , ...,
, ..., 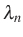 racionálisan lineárisan független valós számok, azaz amelyekhez nincs olyan
racionálisan lineárisan független valós számok, azaz amelyekhez nincs olyan 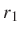 , ...,
, ..., 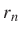 egész számok sorozata, amelyre
egész számok sorozata, amelyre 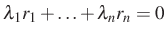 . Legyen
. Legyen 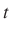 tetszőleges valós szám (az idő). Ekkor a
tetszőleges valós szám (az idő). Ekkor a 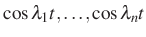 függvénysorozat valószínűség-számítási értelemben is független, például
függvénysorozat valószínűség-számítási értelemben is független, például
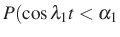 és
és 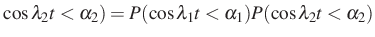
tetszőleges 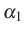 és
és 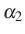 valós számra. Tehát megfelelően skálázott összegükre,
valós számra. Tehát megfelelően skálázott összegükre, -re aszimptotikusan – vagyis elég nagy
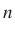 -re – érvényes a Gauss-féle hibatörvény: véletlenül választott
-re – érvényes a Gauss-féle hibatörvény: véletlenül választott 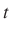 -re
-re 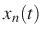 értéke
értéke 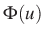 valószínűséggel lesz kisebb, mint
valószínűséggel lesz kisebb, mint 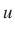 , ahol
, ahol 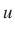 tetszőleges valós szám és
tetszőleges valós szám és 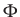 a standard normális eloszlásfüggvény.
a standard normális eloszlásfüggvény.
Érdekességként megemlítem, hogy Kac nem riad vissza a számítógéppel(?) elvégzett numerikus számításoktól sem, pl. numerikusan szemlélteti két függvény függetlenségét két számértékre: 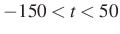 ,
, 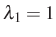 ,
, 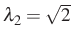 , valamint
, valamint 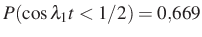 ,
, 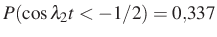 ; és
; és 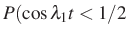 és
és 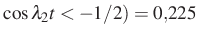 .
.
Valóban, e két esemény valószínűségének szorzata (legalábbis kerekítve) numerikusan egyenlő az együttes valószínűséggel. A 75. oldalon még egy ábra is mutatja a Brown-mozgás kísérleti ábráját.
A matematikától visszatérve az élethez, a harmincas évek középén anyagi és politikai problémáktól tartva, Kac Lengyelországból biztonságosabb helyre akart kivándorolni, családját és menyasszonyát csak később vitte volna maga után. Az Egyesült Királyságba, majd az Egyesült Államokba pályázott állásokra, anélkül, hogy elfogadhatóan tudott volna angolul. Jellemző, hogy amikor két, angol nyelven írott cikkét egy vezető brit matematikai lap elfogadta közlésre, a nagy Hardy megkérte, hogy írja át őket franciára, mert az angolja menthetetlen.
Végül 1938-ban egyéves postdoc-állást kapott a Johns Hopkins Egyetemen (Baltimore), s a II. világháború kitörésekor nem volt hová visszatérnie. Így családja zömétől eltérően, túlélte a holokausztot. Számomra a legmegindítóbb történetpár a következő. A II. világháború után először csak 1959-ben látogatott vissza Lengyelországba. Ott egy gimnáziumi ismerőse elmesélte, hogy szülővárosuk zsidóit több részletben végezték ki a németek, és Kac apjával még a kivégzés előtt sikerült szót váltania. Később Kac tudományos látogatóként eljutott Kijevbe, ahol nehézségek árán ugyan, de visszautazása előtti estén sikerül találkoznia egy jóval fiatalabb lány-unokatestvérével. Alig ismerik meg egymást, és nem tudnak igazán beszélgetni. A találkozás végén az unokatestvér megkérdezi: „akarod-e tudni, mi történt a mieinkkel a német megszállás alatt?” Mielőtt Kac válaszolhatott volna, a rokon folytatta: „jobb, ha nem tudod meg.”
Képzeletben visszatérve Kaccal Amerikába, 1939-ben találkozott Erdős Pállal, akivel elsők között alkalmazták tudatosan a valószínűségszámítást a számelméletben. (Turán Pál már 1934-ben megtette ezt, de csak ösztönösen: újra felfedezve a Csebisev-féle valószínűségszámítási egyenlőtlenséget. Az Erdős–Wintner (1939) számelméleti cikk címében már szintén szerepelt a statisztikai függetlenség.) Kac kiindulása a következő volt: vegyünk két prímszámot, legyenek ezek 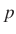 és
és 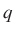 , valamint legyen
, valamint legyen 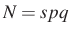 , ahol
, ahol 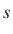 természetes szám. Három valószínűségre vagyunk kíváncsiak. Legyen annak a valószínűsége, hogy egy
természetes szám. Három valószínűségre vagyunk kíváncsiak. Legyen annak a valószínűsége, hogy egy 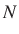 -nél kisebb vagy vele egyenlő természetes szám osztható
-nél kisebb vagy vele egyenlő természetes szám osztható 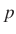 -vel:
-vel: 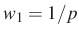 , annak a valószínűsége, hogy egy
, annak a valószínűsége, hogy egy 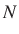 -nél kisebb vagy vele egyenlő természetes szám osztható
-nél kisebb vagy vele egyenlő természetes szám osztható 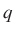 -val:
-val: 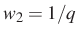 , és annak a valószínűsége, hogy egy
, és annak a valószínűsége, hogy egy 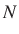 -nél kisebb vagy vele egyenlő természetes szám osztható
-nél kisebb vagy vele egyenlő természetes szám osztható 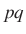 -val:
-val: 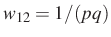 . Ebben az értelemben a
. Ebben az értelemben a 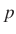 -vel és
-vel és 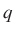 -val való oszthatóság független:
-val való oszthatóság független: 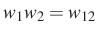 . Kac a prímosztók számának eloszlására volt kíváncsi, és sejtette, hogy itt is a Gauss-törvény érvényesül, de nem tudott egy lényeges szakadékon átlépni. Erdős majdnem végigszunyókálta Kac egyik előadását, amely a véletlen számelméletről szólt. A számelméleti résznél azonban felébredt, és az előadás végén megnyugtatta Kacot, hogy ő majd betemeti a szakadékot. Így is lett. 1940-ben megjelent ötoldalas cikkük egy ideig gyenge visszhangot keltett, de aztán világsikert aratott: a számelmélet új ágát teremtve meg.
. Kac a prímosztók számának eloszlására volt kíváncsi, és sejtette, hogy itt is a Gauss-törvény érvényesül, de nem tudott egy lényeges szakadékon átlépni. Erdős majdnem végigszunyókálta Kac egyik előadását, amely a véletlen számelméletről szólt. A számelméleti résznél azonban felébredt, és az előadás végén megnyugtatta Kacot, hogy ő majd betemeti a szakadékot. Így is lett. 1940-ben megjelent ötoldalas cikkük egy ideig gyenge visszhangot keltett, de aztán világsikert aratott: a számelmélet új ágát teremtve meg.
Kac hamarosan a „világ végén” fekvő, de Borostyán Ligás (elit) Cornell Egyetemen kapott állást: először gyakornok, majd tanársegéd, docens, s végül professzor. Itt lett világhíres kutató. Talán leghíresebb eredménye, amelyet nagyon szerényen ad elő a könyvben, a fizikában központi szerepet játszó Feynman-integrállal kapcsolatos. Biztos nem véletlen, hogy az eredmény kettőjük nevét viseli.
Kiváló ismeretterjesztő volt. Egyik leghíresebb ilyen jellegű cikke: „Hallod-e a dob alakját?” (A találó címet Lipman Bers matematikus javasolta, s ez nagy szerepet játszott a cikk sikerében.) 1963-ban Kac a néhai Hendrik Lorentz holland Nobel-díjas fizikus tiszteletére tartott előadást Leidenben. 1910-ben Lorentz eredetileg azt kérdezte, meg lehet-e határozni a membrán területét a felhangjai alapján. Bár David Hilbert nehéznek vélte a kérdést, de a választ hamar megadta Herman Weyl. Fél évszázaddal később Kac a felhangokból a membrán alakjára szeretett volna következtetni, de a válasz még az önéletrajz megjelenésekor (1985-ben) sem volt ismert. Aztán az 1990-es évek elején kiderült, hogy a válasz nemleges (lásd Wikipédia).
1961-ben Kacot meghívták az elitintézményként alakuló a NY-i Rockefeller Egyetemre, de onnan részben a megszorítások, részben a kötelező nyugdíjazás miatt 1981-ben Los Angelesbe települt át, s ott is halt meg viszonylag hamar, 1984-ben.
Két visszatérő gondolatát emelem ki.
– Nehéz összeegyeztetni az elit- és a tömegoktatás igényeit, de muszáj. Látogatásakor az Oxford Egyetem olyan kiterjedt tutori rendszert működtetett, hogy a felsőbb éveseknek alig maradt idejük a kutatásra. Ugyanakkor a II. világháború idején a Cornell Egyetemen százával kellett megtanítani a műszaki katonákat trigonometriára, és még a matematikailag képzettebb bölcsészoktatókat is be kellett vonni a matematikatanításba.
– Nem szabad elnyomni sem a tiszta, sem az alkalmazott matematikát. Hagyni kell, hogy mindenki azt csinálja, amit szeret. Egyaránt óvakodni kell az öncélú, senkit sem érdeklő matematikától, és a szűklátókörű közvetlen alkalmazások hajszolásától.
Nem folytatom a könyvismertetést. Az egyik legjobb tudományos népszerűsítő könyv, amelyet valaha olvastam. Bölcs, szellemes, időszerű. Le kellene fordítani magyarra!
Köszönetemet fejezem ki Tóth Bálintnak a korábbi változathoz fűzött értékes megjegyzéseiért.
Kapcsolódó recenziók
- Mark Kac: A véletlen rejtélyei - Önéletrajz - Dr. Osman Péter ismertetése (Dr. Osman Péter, http://www.innovacio.hu/, 2023-8-29)
- Alan Turing és Mark Kac, a 21. század két kiemelkedő matematikusa (GReni, https://www.kulturpara.hu/, 2023-4-2)
- Egy matematikus zseni útja Galíciától New York-ig (Haklik Norbert , https://multesjovo.hu/, 2022-06-14)
- Kétfajta nagy tudós létezik: a zseni és a varázsló (Dippold Ádám, https://qubit.hu/, 2022-06-17)
- Mark Kac: A véletlen rejtélyei - ajánló (Szerkesztő, https://ematlap.hu/, 2022-3-2)
- Mihez kezd egy világhírű matematikus az életét átszövő véletlenekkel? (Grozdits Hahó, https://librarius.hu/, 2022-3-6)
- Gondolatok Mark Kac önéletrajzáról (Simonovits András, https://ematlap.hu/konyvespolc-2020-11/980-gondolatok-mark-kac-oneletrajzarol, 2020. június)










